終于知道深度學習機器學習里的微積分需要學哪些知識了
時間：2024-07-23 來源：華清遠見
1. 導數 (Derivatives)
在梯度下降法中使用導數來更新模型參數。
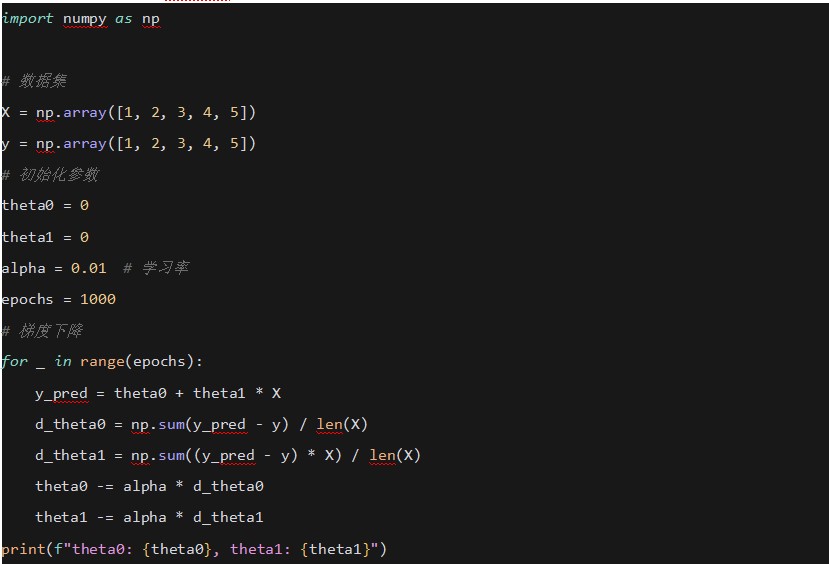
示例
使用Python和NumPy實現簡單的線性回歸梯度下降：
2. 偏導數 (Partial Derivatives)
在神經網絡中使用偏導數來計算每個參數的梯度。
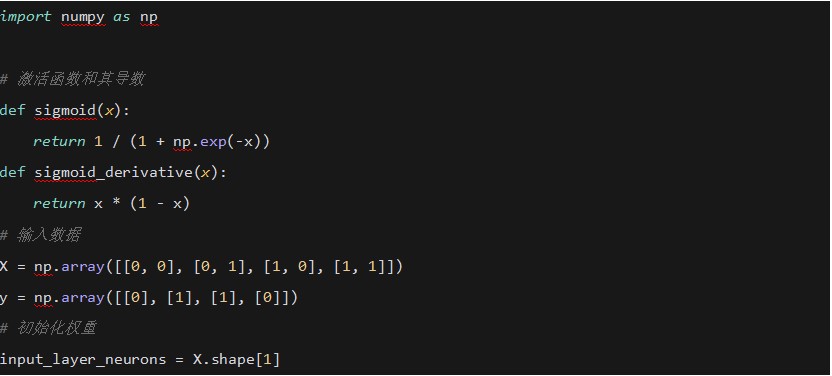
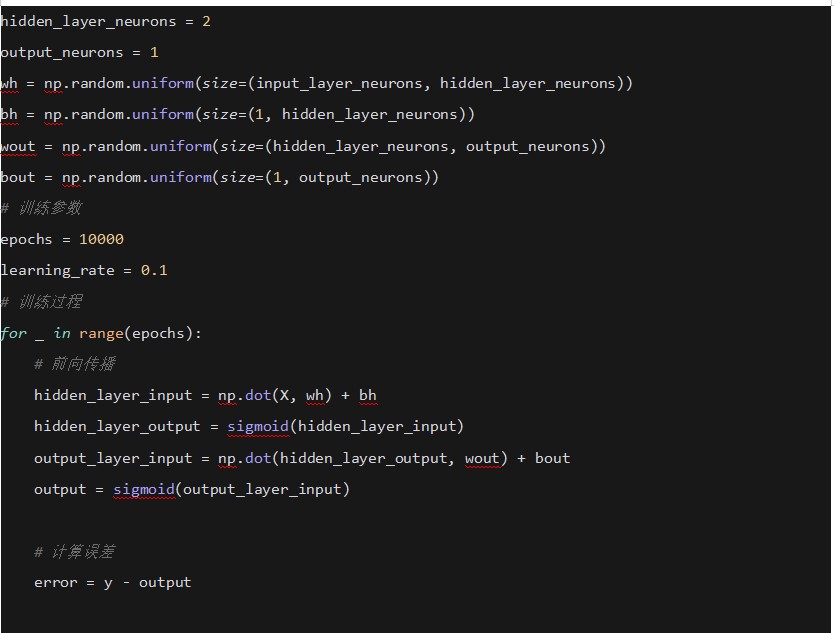
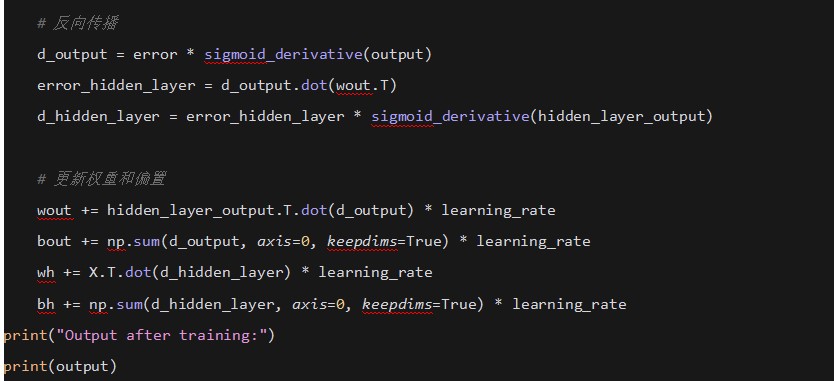
示例
使用Python和NumPy實現簡單的神經網絡反向傳播：
3. 梯度 (Gradient)
在梯度下降法中使用梯度來指示損失函數下降最快的方向。
示例
使用TensorFlow實現線性回歸的梯度下降：
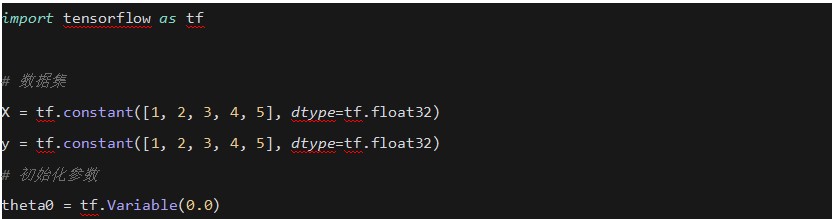
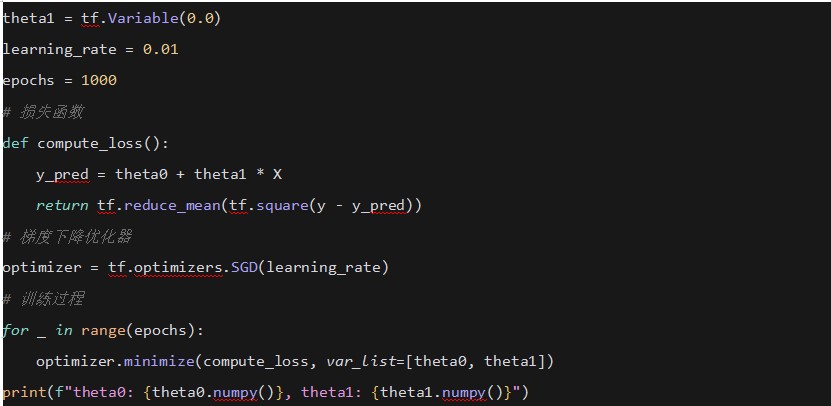
4. 鏈式法則 (Chain Rule)
在反向傳播算法中使用鏈式法則來計算每一層的梯度。
示例
使用PyTorch實現簡單的神經網絡反向傳播：
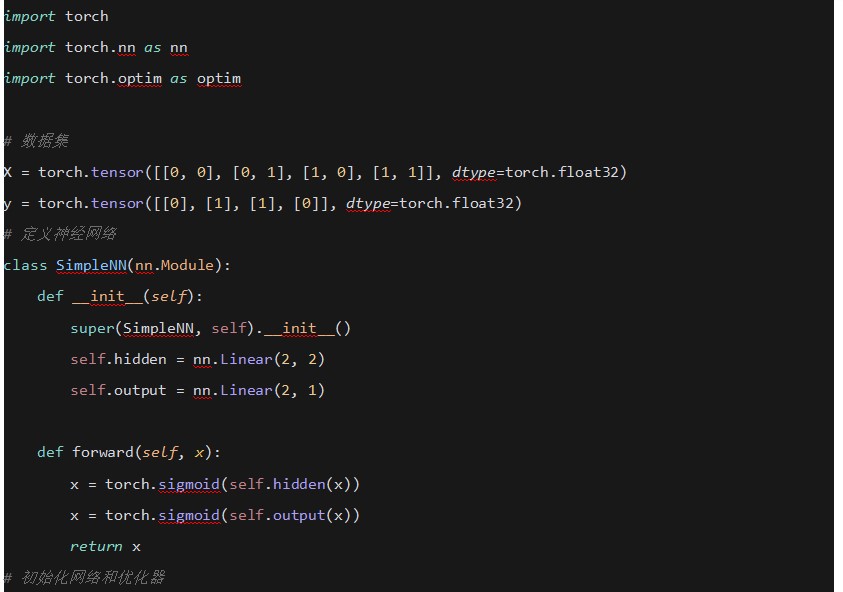
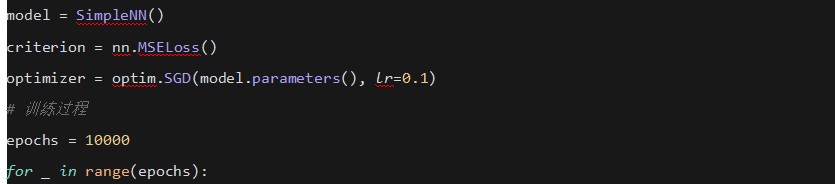
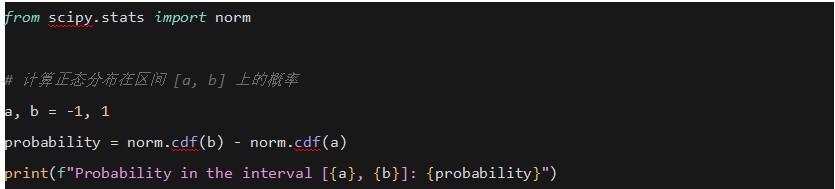
5. 積分 (Integrals)
在概率密度函數中使用積分來計算概率。
示例
使用SciPy計算正態分布的累積分布函數 (CDF)：
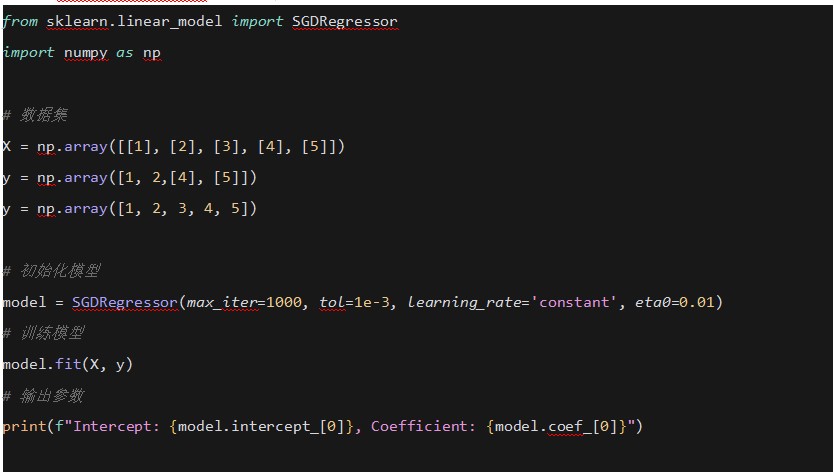
6. 梯度下降法 (Gradient Descent)
使用梯度下降法來最小化損失函數。
示例
使用Scikit-learn實現線性回歸的梯度下降：
總結
這些代碼示例展示了微積分概念在深度學習和機器學習中的實際應用，包括導數、偏導數、梯度、鏈式法則、積分和梯度下降法。通過這些示例，可以更好地理解微積分在優化和訓練模型中的重要性。
